A Bioinformatics Bookmarklet

Sometimes you want to scrape some screen data and analyze it on the spot without copying it to another program. It turns out there's an easy way to do just that. Just highlight the information (by click-dragging the mouse to Select a section of screen data), then run a piece of JavaScript against the selection.

Example: I do a lot of peeking and poking at DNA sequences on the web. Often, I'm interested in knowing various summary statistics for the DNA I'm looking at. For example, I might see a long sequence that looks like AGTTAGAAAACCTCAGCTACTAG (etc.) and wonder what the G+C content of that stream is. So I'll select the text by click-dragging across it. Then I'll obtain the text in JavaScript by calling getSelection().toString(). Then I parse the text and display the results in an alert dialog.

Suppose I've selected a run of DNA on-screen and I want to know the base content (the amounts of G, C, T, and A).

text = getSelection().toString(); // get the data as a string
text = text.toUpperCase(); // optionally convert it to upper case

bases = new Object;  // create a place to store the base counts
bases.G = bases.C = bases.T = bases.A = 0; // initialize

// now loop over the string contents:
for (var i = 0; i < text.length; i++)
   bases[ text[i] ]++;  // bump the count for that base

// format the data for viewing

msg = "G: " + bases.G/text.length + "\n";

msg += "C: " + bases.C/text.length + "\n";

msg += "A: " + bases.A/text.length + "\n";

msg += "T: " + bases.T/text.length + "\n";

msg += "GC Content: " + (bases.G + bases.C)/text.length; 

// view it:

alert( msg ); 

If I run this script against a web page where I've highlighted some DNA text, I get:

 

The nice part is, you can put the above code in a bookmarklet, associate the bookmarklet with a button, and keep it in your bookmark bar so that whenever you want to run the code, you can just point and click. To do the packaging, reformat the above code (or your modified version of it) as a single line of code preceded by "javascript:" (don't forget the colon), then set that code as the URL of a bookmark. Instead of going to a regular URL, the browser will see "javascript:" as the URL scheme and execute the code directly.

Bookmarklets of this sort have proven to be a major productivity boon for me in various situations as I cruise the web. When I see data I want to analyze, I don't have to copy and paste it to Excel (or whatever). With a bookmarklet, I can analyze it instantly, sur la vitre.

A Very Simple Test of Chargaff's Second Rule

We know that for double-stranded DNA, the number of purines (A, G) will always equal the number of pyrimidines (T, C), because complementarity depends on A:T and G:C pairings. But do purines have to equal pyrimidines in single-stranded DNA? Chargaff's second parity rule says yes. Simple observation says no.

Suppose you have a couple thousand single-stranded DNA samples. All you have to do to see if Chargaff's second rule is correct is create a graph of A versus T, where each point represents the A and T (adenine and thymine) amounts in a particular DNA sample. If A = T (as predicted by Chargaff), the graph should look like a straight line with a slope of 1:1.

For fun, I grabbed the sequenced DNA genome of Clostridium botulinum A strain ATCC 19397 (available from the FASTA link on this page; be ready for a several-megabyte text dump), which contains coding sequences for 3552 genes of average length 442 bases each, and for each gene, I plotted the A content versus the T content.

A plot of thymine (T) versus adenine (A) content for all 3552 genes in C. botulinum coding regions. The greyed area represents areas where T/A > 1. Most genes fall in the white area where A/T > 1.

As you can see, the resulting cloud of points not only doesn't form a straight line of slope 1:1, it doesn't even cluster on the 45-degree line at all. The center of the cluster is well below the 45-degree line, and (this is the amazing part) the major axis of the cluster is almost at 90 degrees to the 45-degree line, indicating that the quantity A+T tends to be conserved.

A similar plot of G versus C (below) shows a somewhat different scatter pattern, but again notice that the centroid of the cluster is well off the 45-degree centerline. This means Chargaff's second rule doesn't hold (except for the few genes that randomly fell on the centerline).

A plot of cytosine (C) versus guanine (G) for all genes in all coding regions of C. botulinum. Again, notice that the points cluster well away from the 45-degree line (where they would have been expected to cluster, according to Chargaff).

The numbers of bases of each type in the botulinum genome are:

G: 577108
C: 358170
T: 977095
A: 1274032

Amazingly, there are 296,937 more adenines than thymines in the genome (here, I'm somewhat sloppily equating "genome" with combined coding regions). Likewise, excess guanines number 218,938. On average, each gene contains 73 excess purines (42 adenine and 31 guanine).

The above graphs are in no way unique to C. botulinum. If you do similar plots for other organisms, you'll see similar results, with excess purines being most numerous in organisms that have low G+C content. As explained in my earlier posts on this subject, the purine/pyrimidine ratio (for coding regions) tends to be high in low-GC organisms and low in high-GC organisms, a relationship that holds across all bacterial and eukaryotic domains.

Chargaff's Second Parity Rule is Broadly Violated

Erwin Chargaff, working with sea-urchin sperm in the 1950s, observed that within double-stranded DNA, the amount of adenine equals the amount of thymine (A = T) and guanine equals cytosine (G = C), which we now know is the basis of "complementarity" in DNA. But Chargaff later went on to observe the same thing in studies of single-stranded DNA, causing him to postulate that A = T and G = C more generally (within as well as across strands of DNA). The more general postulation is known as Chargaff's second parity rule. It says that A = T and G = C within a single strand of DNA.

The second parity rule seemed to make sense, because there was and is no a priori reason to think that DNA or RNA, whether single-stranded or double-stranded, should contain more purines than pyrimidines (nor vice versa). All other factors being equal, nature should not "favor" one class of nucleotide over another. Therefore, across evolutionary times frames, one would expect purine and pyrimidine prevalences in nucleic acids to equalize.

What we instead find, if we look at real-world DNA and RNA, is that individual strands seldom contain equal amounts of purines and pyrimidines. Szybalski was the first to note that viruses (which usually contain single-stranded nucleic acids) often contain more purines than pyrimidines. Others have since verified what Szybalski found, namely that in many organisms, DNA is purine-heavy on the "sense" strand of coding regions, such that messenger RNA ends up richer in purines than pyrimidines. This is called Szybalski's rule.

In a previous post, I presented evidence (from analysis of the sequenced genomes of 93 bacterial genera) that Szybalski's rule not only is more often true than Chargaff's second parity rule, but in fact purine-loading of coding region "message" strands occurs in direct proportion to the amount of A+T (or in inverse propoertion to the amount of G+C) in the genome. At G+C contents below about 68%, DNA becomes heavier and heavier with purines on the message strand. At G+C contents above 68%, we find organisms in which the message strand is actually pyrimidine-heavy instead of purine-heavy.

I now present evidence that purine loading of message strands in proportion to A+T content is a universal phenomenon, applying to a wide variety of eukaryotic ("higher") life forms as well as bacteria.

According to Chargaff's second parity rule, all points on this graph should fall on a horizontal line at y = 1. Instead, we see that Chargaff's rule is violated for all but a statistically insignificant subset of organisms. Pink/orange points represent eukaryotic species. Dark green data points represent bacterial genera. See text for discussion. Permission to reproduce this graph (with attribution) is granted.

To create the accompanying graph, I did frequency analysis of codons for 58 eukaryotic life forms (pink data points) and 93 prokaryotes (dark green data points) in order to derive prevalences of the four bases (A, G, C, T) in coding regions of DNA. Eukaryotes that were studied included yeast, molds, protists, warm and cold-blooded animals, flowering and non-flowering plants, alga, and insects and crustaceans. The complete list of organisms is shown in a table further below.

It can now be stated definitively that Chargaff's second parity rule is, in general, violated across all major forms of life. Not only that, it is violated in a regular fashion, such that purine loading of mRNA increases with genome A+T content. Significantly, some organisms with very low A+T content (high G+C content) actually have pyrimidine-loaded mRNA, but they are in a small minority.

Purine loading is both common and extreme. For about 20% of organisms, the purine-pyrimidine ratio is above 1.2. For some organisms, the purine excess is more than 40%, which is striking indeed.

Why should purines migrate to one strand of DNA while pyrimidines line up on the other strand? One possibility is that it minimizes spontaneous self-annealing of separated strands into secondary structures. Unrestrained "kissing" of intrastrand regions during transcription might lead to deleterious excisions, inversions, or other events. Poly-purine runs would allow the formation of many loops but few stems; in general, secondary structures would be rare.

The significance of purine loading remains to be elucidated. But in the meantime, there can be no doubt that purine enrichment of message strands is indeed widespread and strongly correlates to genome A+T content. Chargaff's second parity rule is invalid, except in a trivial minority of cases.

The prokaryotic organisms used in this study were presented in a table previously. The eukaryotic organisms are shown in the following table:

Organism	Comment	G+C%	Purine ratio
Chlorella variabilis strain NC64A	endosymbiont of Paramecium	68.76	1.1055181128896376
Chlamydomonas reinhardtii strain CC-503 cw92 mt+	unicellular alga	67.96	1.0818749999999997
Micromonas pusilla strain CCMP1545	unicellular alga	67.41	1.1873268193087356
Ectocarpus siliculosus strain Ec 32	alga	62.74	1.2090728330510347
Sporisorium reilianum SRZ2	smut fungus	62.5	0.9776547360094916
Leishmania major strain Friedlin	protozoan	62.47	1.0325
Oryza sativa Japonica Group	rice	54.77	1.0668412348401317
Takifugu rubripes (torafugu)	fish	54.08	1.0655094027691674
Aspergillus fumigatus strain A1163	fungus	53.89	1.013091641490433
Sus scrofa (pig)	pig	53.77	1.0680595779892428
Drosophila melanogaster (fruit fly)		53.69	1.0986989367655287
Brachypodium distachyon line Bd21	grass	53.32	1.0764746703677999
Selaginella moellendorffii (Spikemoss)	moss	52.83	1.1014492753623195
Equus caballus (horse)	horse	52.29	1.0844453711426192
Pongo abelii (Sumatran orangutan)	orangutan	52	1.0929015146227405
Homo sapiens	human	51.97	1.0939049081896255
Mus musculus (house mouse) strain mixed	mouse	51.91	1.0827720297201582
Tuber melanosporum (Perigord truffle) strain Mel28	truffle	51.4	1.0836820083682006
Phaeodactylum tricornutum strain CCAP 1055/1	diatom	51.06	1.0418452745458253
Arthroderma benhamiae strain CBS 112371	fungus	50.99	1.0360268674944024
Ornithorhynchus anatinus (platypus)	platypus	50.97	1.1121909993661525
Taeniopygia guttata (Zebra finch)	bird	50.81	1.1344717182497328
Trypanosoma brucei TREU927	sleeping sickness protozoan	50.78	1.106974784013486
Danio rerio (zebrafish) strain Tuebingen	fish	49.68	1.1195053003533566
Gallus gallus	chicken	49.54	1.1265418970650787
Monodelphis domestica (gray short-tailed opossum)	opossum	49.07	1.0768110918544194
Sorghum bicolor (sorghum)	sorghum	48.93	1.046422719825232
Thalassiosira pseudonana strain CCMP1335	diatom	47.91	1.1403183213189638
Hyaloperonospora arabidopsis	mildew	47.75	1.053039546400631
Daphnia pulex (common water flea)	water flea	47.57	1.058036633052068
Physcomitrella patens subsp. patens	moss	47.33	1.1727134477514667
Anolis carolinensis (green anole)	lizard	46.72	1.113765477057538
Brassica rapa	flowering plant	46.29	1.1056659411640803
Fragaria vesca (woodland strawberry)	strawberry	46.02	1.1052853232259425
Amborella trichopoda	flowering shrub	45.88	1.0992441209406494
Citrullus lanatus var. lanatus (watermelon)	watermelon	44.5	1.0855134984692458
Capsella rubella	mustard-family plant	44.37	1.1041257367387034
Arabidopsis thaliana (thale cress)	cress	44.15	1.109853013573388
Lotus Japonicus	lotus	44.11	1.0773228019122847
Populus trichocarpa (Populus balsamifera subsp. trichocarpa)	tree	43.7	1.1097672456226706
Cucumis sativus (cucumber)	cucumber	43.56	1.0823847862298719
Caenorhabditis elegans strain Bristol N2	worm	42.96	1.106320224719101
Vitis vinifera (grape)	grape	42.75	1.0859833393697935
Ciona intestinalis	tunicate	42.68	1.158652461848546
Solanum lycopersicum (tomato)	tomato	41.7	1.1177
Theobroma cacao (chocolate)	chocolate	41.31	1.1297481860862142
Medicago truncatula (barrel medic) strain A17	flowering plant	40.78	1.093754366354618
Apis mellifera (honey bee) strain DH4	honey bee	39.76	1.216042543762464
Saccharomyces cerevisiae (bakers yeast) strain S288C	yeast	39.63	1.1387641650630744
Acyrthosiphon pisum (pea aphid) strain LSR1	aphid	39.35	1.1651853457619772
Debaryomyces hansenii strain CBS767	yeast	37.32	1.1477345930856775
Pediculus humanus corporis (human body louse) strain USDA	louse	36.57	1.2365791828213537
Schistosoma mansoni strain Puerto Rico	trematode	35.94	1.0586902800658977
Candida albicans strain WO-1	yeast	35.03	1.1490291609944834
Tetrapisispora phaffii CBS 4417 strain type CBS 4417	yeast	34.69	1.17503805175038
Paramecium tetraurelia strain d4-2	protist	30.03	1.2494922903347117
nucleomorph Guillardia theta	endosymbiont	23.87	1.1529462427330803
Plasmodium falciparum 3D7	malaria parasite	23.76	1.4471365638766511

Chargaff's Second Parity Rule is Violated in Proportion to Genome A+T Content

Erwin Chargaff was the first to notice, in the early 1950s, before Watson and Crick deduced the structure of DNA, that the quantity of purines in DNA equals the quantity of pyrimidines (specifically, the amount of adenine equals the amount of thymine; and the amount of guanine equals the amount of cytosine). This observation was key to establishing the structure of DNA, and it is often cited as Chargaff's first parity rule. But Chargaff also made another observation (the second parity rule), namely that even within a single strand of DNA, the amount of adenine tends to equal the amount of thymine and the amount of guanine tends to equal the amount of cytosine.

It's easy to understand why the first parity rule holds true, because complementarity of DNA strands depends on A pairing with T and G pairing with C; these pairings give rise to the "rungs" of the DNA ladder and ensure that copying of strands occurs with total fidelity during cell division. But there doesn't seem to be any a priori reason why the second parity rule should hold true. And in fact, it often doesn't hold true, as Wacław Szybalski noted in 1966 when he reported finding imbalances of purines and pyrimidines in bacteriophage and other DNA samples. Szybalski observed that in most cases, protein-coding regions of DNA tend to have slightly more purines than pyrimidines on one strand and slightly more pyrimidines than purines on the other strand, such that messenger RNA ends up purine-heavy.

If you're having trouble visualizing the situation, imagine a very short (12-base) "chromosome" containing 50% G+C content. One possibility is that one strand looks like GGGGGGTTTTTT and the other strand is CCCCCCAAAAAA. In this case half the purines (all the G's) are on one strand and half (A's) are on the other. But you could just as easily have strands be GGGGGGAAAAAA and CCCCCCTTTTTT. In this case, one strand is all-purines, the other all-pyrimidines. Both examples violate Chargaff's second rule, which requires that G = C and A = T within each strand (e.g., GGGCCCTTTAAA + CCCGGGAAATTT would obey the rule).

To my knowledge, no one has yet reported the fact (which I'll now report) that the degree to which Chargaff's second parity rule is violated depends on the G+C content of the source genome (at least for bacteria). Simply put, organisms with a G+C content of around 68% obey Chargaff's rules. Organisms with more than 68% G+C content violate Chargaff's second rule in the direction of pyrimidine loading of mRNA. Organisms with less than 68% G+C content (which of course includes the overwhelming majority of organisms) have purine-heavy DNA, to a degree that depends on the amount of A+T in the DNA.

Purine/pyrimidine ratio (in coding regions) as a function of genome G+C content based on codon analysis of 93 organisms. As genomes become more A+T rich, mRNA becomes more heavily purine-loaded.

The above graph shows how this relationship works. To create the graph, I did a statistical analysis of codon usage in 93 bacterial species. Organisms were chosen so as to obtain representatives across the AT/GC spectrum. No genus is represented more than once. In order to get as broad a sampling as possible, I included 14 intracellular symbionts with ultra-low G+C content (plus one such creature—Candidatus Hodgkinia cicadicola—with a 58% G+C content); many extremophiles; heterotrophs and autotrophs; pathogens and non-pathogens; and organisms with large and small genomes. The complete organism list is presented in a table further below.

Codon usage statistics for each organism were obtained using tools at http://genomevolution.org. Relative prevalences of A, T, G, and C in the genomes' coding regions were determined by codon frequency analysis. The purine:pyrimidine ratio was simply calculated as (A+G)/(C+T) based on the codon-wise frequency of usage of each base.

What we see is that while there is a good deal of noise in the data, nevertheless it's quite clear that purine/pyrimidine ratios increase sharply as genome G+C decreases.Organisms for which Chargaff's second rule holds true (points falling at y = 1.0) are in a small minority. Most organisms have purine-rich coding regions, resulting in purine-rich mRNA.

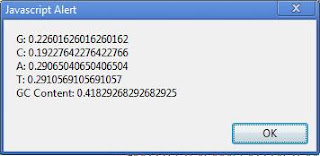
Purine enrichment occurs for both adenine and guanine. For example, in Clostridium botulinum (genome G+C = 28.21%), codon analysis reveals G/C/A/T relative abundances (on the coding strand) of 18.3/10.8/40.3/30.6.

Intra-codon base position analysis reveals that purine enrichment is far more concentrated in position one of the codon than other positions. The graphs below show the purine balance on a position-by-position basis, for each base in a codon.

Most of the variation in purine/pyrimidine ratio happens in position 1 of the codon (the 'A' in ATG, for example). Notice that the purine/pyrimidine ratio in this position is well above 1.0 for all organisms.

Variation in purine loading at the second position of the codon is more carefully controlled (notice that there is less "scatter" in this graph). The y-axis scale is different here than in the previous graph, hence the slope is quite a bit less pronounced than it looks. Also, notice that most of the points in this plot are below parity (i.e., below 1.0 on the y-axis), indicating that this codon position is relatively pyrimidine-rich.

The third (so-called "wobble") position of the codon shows considerable variation in values, but the slope of the curve is less than in the previous two graphs, and this position is pyrimidine-rich for about two-thirds of the organisms.

It's well known that GC-skew tends to be exaggerated in position 3 of the codon. For example, if the overall genome G+C is 70%, the position-wise G+C for the wobble base may be 90%. Surprisingly, we find that purine loading is most exaggerated in position 1 of the codon, not position 3. Not only is the slope of the purine-ratio curve shallower in position 3 than for the other two base positions, only position 1 is actually purine-heavy: positions 2 and 3 tend to be net pyrimidine-rich. This fact (that purine loading is primarily localized to codon position 1, whereas GC-skew is exaggerated in position 3) might indicate that the forces responsible for purine loading are entirely different from the forces responsible for GC skew.

What might those forces be? What kinds of selection pressure might cause organisms to purine-load one strand of their DNA? One possibility is that purine loading of the coding strand is a strategy for protecting the "weaker" or more vulnerable strand from damage or mutations. Cytosine is thought to be particularly vulnerable to deamination (and later substitution with thymine, during repair). It's possible that the transcription process (which is asymmetric, in that RNA polymerase operates against just one strand of DNA, leaving the other strand free) is protective of the antisense strand of DNA. That is, in transcription, RNA polymerase cloaks the antisense strand and in so doing renders that strand less vulnerable to deamination events, rogue methylations, etc., while transcription is taking place.

An entirely different possibility is envisioned by an RNA World hypothesis. In this hypothesis, the genetic material of early ancestor organisms was single-stranded RNA. Since single-stranded RNA is not "complementary" to anything, there is no need for it to obey Chargaff symmetries. Thus, purine loading could have occurred prior to the advent of double-stranded DNA, and early organisms could have been uniformly AT-rich. In this model of the world, GC-rich genomes are a late development, and the processes responsible for creating GC-rich DNA led to genetic material with full Chargaff base parity.

We may not know for a long time (if ever) what the mechanisms of purine enrichment are. But we know for sure that purine accumulation is a widespread phenomenon in the bacterial world (operating across diverse clades) and happens in a way that encourages purine-rich mRNA in organisms with low G+C content in their genomes.


Organisms used in this study:

Organism	GC%	genome size
Anaeromyxobacter dehalogenans 2CP-1	74.67	5009007
Cellulomonas flavigena strain DSM 20109	74.29	4123179
Xylanimonas cellulosilytica strain DSM 15894	72.47	3831380
Streptomyces bingchenggensis strain BCW-1	70.75	11936683
Myxococcus fulvus strain HW-1	70.63	9003593
Rubrobacter xylanophilus strain DSM 9941	70.48	3225748
Rhodospirillum centenum ATCC 51521	70.46	4355543
Actinomyces sp. oral taxon 175 strain F0384	68.73	3133330
Rhodococcus equi strain ATCC 33707	68.72	5259057
Acidovorax avenae subsp. citrulli strain AAC00-1	68.53	5352772
Bordetella bronchiseptica strain RB50	68.08	5339179
Alicycliphilus denitrificans strain K601	67.81	5070751
Stenotrophomonas maltophilia strain JV3	66.89	4544477
Rhodobacter capsulatus strain SB 1003	66.56	3871920
Pseudomonas aeruginosa strain PA7	66.45	6588339
Ralstonia eutropha strain H16	66.29	7416678
Xanthomonas campestris pv. raphani strain 756C	65.29	4941214
Thioalkalivibrio sp. strain HL-EbGR7	65.06	3470516
Rhodopseudomonas palustris strain BisB18	64.96	5513844
Brevundimonas diminuta strain ATCC 11568	64.51	3369316
Rhodothermus marinus strain DSM 4252	64.09	3386737
Bradyrhizobium japonicum strain USDA 110	64.06	9105828
Mycobacterium tuberculosis strain C	63.82	4379118
Thermanaerovibrio acidaminovorans strain DSM 6589	63.79	1848474
Halomonas elongata DSM 2581 strain type DSM 2581	63.61	4061296
Novosphingobium nitrogenifigens strain DSM 19370	63.43	4182647
Polaromonas sp. strain JS666	62.24	5898676
Desulfovibrio africanus strain Walvis Bay	61.42	4200534
Candidatus Desulforudis audaxviator strain MP104C	60.85	2349476
Burkholderia rhizoxinica strain HKI 454	60.68	3750138
Slackia heliotrinireducens strain DSM 20476	60.21	3165038
Candidatus Nitrospira defluvii	59.03	4317083
Halogeometricum borinquense DSM 11551	58.43	3944467
Candidatus Hodgkinia cicadicola strain Dsem	58.39	143795
Sideroxydans lithotrophicus strain ES-1	57.54	3003656
Cenarchaeum symbiosum A	57.37	2045086
Serratia sp. strain AS12	55.96	5443009
Acidaminococcus fermentans strain DSM 20731	55.84	2329769
Hyperthermus butylicus strain DSM 5456	53.74	1667163
Methanosaeta thermophila (Methanothrix thermophila PT) strain PT	53.55	1879471
Neisseria gonorrhoeae strain NCCP11945	53.37	2236178
Treponema paraluiscuniculi strain Cuniculi A	52.74	1133390
Pseudovibrio sp. strain FO-BEG1	52.38	5916782
Nitrosococcus halophilus strain Nc4	51.60	4145260
Herpetosiphon aurantiacus DSM 785	50.84	6785430
Escherichia coli B strain REL606	50.77	4629812
Bdellovibrio bacteriovorus strain ATCC15356;	50.65	3782950
Pectobacterium wasabiae strain WPP163	50.48	5063892
Anaplasma centrale (Anaplasma marginale subsp. centrale str. Israel) strain Israel	49.98	1206806
Actinomyces coleocanis strain DSM 15436	49.47	1723843
Desulfotalea psychrophila strain LSv54	46.72	3659634
Polynucleobacter necessarius strain STIR1	45.56	1560469
Nitrosomonas sp. strain Is79A3	45.44	3783444
Coprothermobacter proteolyticus strain DSM 5265	44.77	1424912
Vibrio sp. Ex25 strain EX25	44.57	5160431
Geobacillus thermoglucosidans strain TNO-09.020	43.82	3740238
Waddlia chondrophila strain 2032/99	43.59	2139757
Bacteroides fragilis strain 638R	43.42	5373121
Thiomicrospira crunogena strain XCL-2	43.13	2427734
Coxiella burnetii strain CbuG_Q212	42.63	2008870
Chlamydia muridarum Nigg strain MoPn	40.27	1080451
Psychromonas ingrahamii strain 37	40.09	4559598
Nitratiruptor sp. strain SB155-2	39.69	1877931
Lactobacillus reuteri strain DSM 20016	38.87	1999618
Thermotoga lettingae strain TM	38.70	2135342
Streptococcus pyogenes strain Alab49	38.63	1841271
Bartonella bacilliformis strain ATCC 35685; KC583	38.24	1445021
Halothermothrix orenii strain DSM 9562; H 168	37.78	2463968
Staphylothermus marinus strain F1	35.73	1570485
Calditerrivibrio nitroreducens strain DSM 19672	35.69	2216552
Bacillus thuringiensis serovar andalousiensis strain BGSC 4AW1	34.96	5488844
Desulfurobacterium thermolithotrophum	34.95	1541968
Wolbachia pipientis strain wPip	34.19	1482455
Nitrosopumilus maritimus strain SCM1	34.17	1645259
Staphylococcus aureus strain 04-02981	32.90	2821452
Methanobrevibacter ruminantium strain M1	32.64	2937203
Rickettsia japonica strain YH	32.35	1283087
Methanocaldococcus fervens strain AG86 (v1)	32.21	1507251
Mycoplasma genitalium G37 strain G-37	31.69	580076
Nanoarchaeum equitans strain Kin4-M	31.56	490885
Orientia tsutsugamushi strain Boryong	30.53	2127051
Methanococcus aeolicus strain Nankai-3	30.04	1569500
Candidatus Pelagibacter ubique strain HTCC1062	29.68	1308759
Ehrlichia canis strain Jake	28.96	1315030
Arcobacter nitrofigilis strain DSM 7299	28.36	3192235
Clostridium botulinum A strain ATCC 19397	28.21	3863450
Parvimonas sp. oral taxon 393 strain F0440	28.17	1483165
Candidatus Arthromitus sp. strain SFB-mouse-NYU	27.94	1569870
Candidatus Blochmannia floridanus	27.38	705557
Buchnera aphidicola (Acyrthosiphon pisum) strain 5A	25.69	653223
Wigglesworthia glossinidia endosymbiont of Glossina brevipalpis	22.48	703004
Candidatus Sulcia muelleri strain CARI (v1)	21.13	276511
Candidatus Carsonella ruddii strain PV (v1)	16.56	159662

DNA: Full of Surprises

DNA is full of surprises, one of them being the radically different ways in which it can be used to express information. We think of DNA as a four-letter language (A,T,G,C), but some organisms choose to "speak" mostly G and C. Others avoid G and C, preferring instead to "speak" A and T. The question is, if DNA is fundamentally a four-letter language, why would some organisms want to limit themselves to dialects that use mostly just two letters?

The DNA of Clostridium botulinum (the botulism bug; a common soil inhabitant) is extraordinarily deficient in G and C: over 70% of its DNA is A and T. The soil bacterium Anaeromyxobacter dehalogenans, on the other hand, has DNA that's 74% G and C. Think of the constraints this puts on a coding system. Imagine that you want to store data using a four-letter alphabet, but you are required to use two of the four letters 74% of the time! Suddenly a two-bit-per-symbol encoding scheme (a four-letter code) starts to look and feel a lot more like a one-bit-per-symbol (two-letter) scheme.

What kinds of information are actually stored in DNA? Several kinds, but bottom line, DNA is primarily a system for specifying sequences of amino acids. The information is stored as three-letter "words" (GCA, ATG, TCG, etc.) called codons. There are 64 possible length-3 words in a system that uses a 4-letter alphabet. Fortunately, there are only 20 amino acids. I say "fortunately," because imagine if there were 64 different amino acids (as there might be in extra-terrestrial life, say) and they had to occur in roughly equal amounts in all proteins. Every possible codon would have to be used (in roughly equal numbers) and there would be no possibility of an organism like C. botulinum developing a "preference" for A or T in its DNA. It is precisely because only 20 codons out of a possible 64 need be used that organisms like C. botulinum (with a huge imbalance of AT vs. GC in its DNA) can exist.

As it happens, all organisms do tend to use all 64 possible codons, but they use them with vastly varying frequencies, giving rise to codon "dialects." (Note that the mapping of 64 codons onto 20 amino acids means some codons are necessarily synonymous. For example, there are four different codons for glycine and six for leucine.) You might expect that an organism like C. botulinum with mostly A and T in its DNA would "speak" in A- and T-rich codons. And you'd be right. Here's a chart showing which codons C. botulinum actually uses, and at what frequencies:

The green-highlighted codons are the ones C. botulinum uses preferentially (with the usage frequencies shown as precentages). As you can see, the most-often-used codons tend to contain a lot of A and/or T. Which is exactly what you'd expect, given that the organism's DNA is 72% A and T.

In theory, a 3-letter word in a 4-letter language can store six bits of information. But we know from information theory that the actual information content of a word depends on how often it's used. If I send you a 100-word e-mail that contains the question "Why?" repeated 100 times, you're not really receiving the same amount of information as would be in a 100-word e-mail that contains text in which no word appears twice.

The average information content of a C. botulinum codon is easily calculated using the usage-frequencies shown above. (All you do is calculate -F * log₂(F) for each codon and add up the results.) If you do the math, you find that C. botulinum uses an average of 5.217 bits per codon, about 13% short of the theoretical six bits available.

One might imagine that the more GC/AT-imbalanced an organism's DNA is, the more biased its codon preferences will be. This is exactly what we find if we plot codon entropy against genome G+C content for a range of organisms having DNA of various G+C contents.

Average codon entropy versus genome G+C content for 90 microorganisms.

In the above graph, you can see that when an organism's DNA is composed of equal amounts of the bases (G+C = 50%, A+T = 50%), the organism tends to use all codons more or less equally, and entropy approaches the theoretical limit of six bits per codon. But when an organism develops a particular "dialect" (of GC-rich DNA, or AT-rich DNA), it starts using a smaller and smaller codon vocabulary more and more intensively. This is what causes the curve to fall off sharply on either side of the graph.

If you have an observant eye, you may have noticed that the two halves of the graph are not symmetrical, even though they look symmetrical at first glance. (Organisms on the high-GC side are using slightly less entropy per codon than low-GC organisms, for a given amount of genome GC/AT skew.) If you're a biologist, you might want to think about why this is so. I'll return to the subject in a future post.